在当今数字化时代,矩阵计算在众多领域都有着广泛应用。maple作为一款强大的数学软件,为方形矩阵的计算提供了便捷高效的解决方案。
矩阵的创建
首先,我们来看如何在maple中创建方形矩阵。例如,要创建一个3x3的矩阵,可以使用以下代码:
```
a := matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]);
```
这样就成功创建了一个3阶方形矩阵a。
矩阵的基本运算
1. 加法:若有另一个3x3矩阵b,如`b := matrix([[9, 8, 7], [6, 5, 4], [3, 2, 1]])`,那么矩阵a与b的加法运算为`a + b`。
2. 乘法:矩阵乘法也很简单,例如a乘以自身`a &* a`就能得到结果。
矩阵的行列式计算
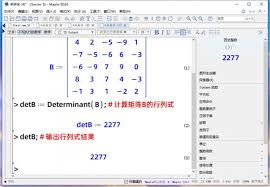
计算矩阵的行列式是一个重要操作。对于矩阵a,只需使用`det(a)`命令,就能快速得出其行列式的值。
矩阵的逆
求矩阵的逆同样方便。若矩阵a可逆,使用`linearalgebra[inverse](a)`就能得到其逆矩阵。
特征值与特征向量
maple还能轻松计算矩阵的特征值与特征向量。对于矩阵a,使用`eigenvectors(a)`命令,就能同时得到特征值和对应的特征向量。
通过这些实例可以看出,maple在方形矩阵计算方面表现出色。无论是简单的矩阵创建、基本运算,还是复杂的行列式计算、求逆以及特征值与特征向量的求解,都能快速准确地完成。它为科研工作者、工程师以及学生等提供了极大的便利,帮助他们在矩阵相关的数学问题上节省时间和精力,更高效地进行研究和学习。






















