线性代数作为数学领域的重要分支,在众多科学与工程领域有着广泛应用。然而,复杂的线性代数计算常常让人望而却步。maple软件的出现,为解决线性代数问题提供了强大而便捷的工具。
maple具有丰富的线性代数函数库,能够轻松处理矩阵运算。无论是矩阵的加法、减法、乘法,还是求矩阵的逆、行列式、秩等,都只需简单的命令即可完成。例如,要计算一个3x3矩阵a的行列式,只需在maple中输入“det(a)”,瞬间就能得到结果。这大大节省了手动计算的时间和精力,减少了出错的可能性。
在求解线性方程组方面,maple表现得同样出色。给定一个线性方程组,我们可以直接将其系数矩阵和常数项输入maple,通过简单的指令就能求出方程组的解。比如对于方程组:
⁄[
⁄begin{cases}
2x + 3y = 5 ⁄⁄
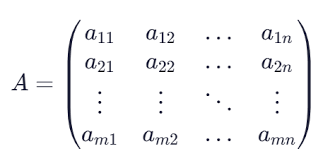
4x - y = 3
⁄end{cases}
⁄]
在maple中输入相应的矩阵和指令,就能快速得到⁄(x = 1⁄),⁄(y = 1⁄)的准确解。
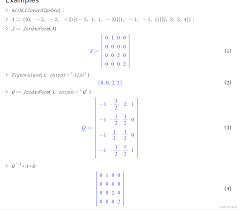
maple还擅长处理特征值和特征向量问题。对于一个给定的矩阵,使用“eigenvects”命令,就能求出其所有的特征值及对应的特征向量。这对于分析矩阵的性质、解决实际问题中的动态系统等有着重要意义。
此外,maple在处理向量空间相关问题时也十分高效。它可以方便地进行向量的线性组合、求向量的正交补等操作。通过这些功能,我们能够深入研究向量空间的结构和性质。
使用maple解决线性代数问题,不仅提高了计算效率,还能确保结果的准确性。它让我们从繁琐的线性代数计算中解脱出来,将更多的精力投入到对问题的分析和理解上。无论是学生学习线性代数课程,还是科研人员在实际工作中遇到线性代数问题,maple都能成为得力的助手,帮助我们轻松攻克线性代数的难关,开启数学探索的新征程。让我们借助maple的强大功能,更加深入地领略线性代数的魅力,解决更多实际问题。






















