数学表达式是数学学习和应用中的重要组成部分,掌握正确的计算方法至关重要。
遵循运算顺序
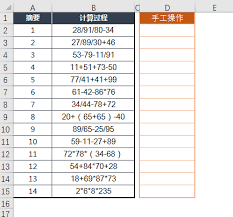
先乘除后加减,有括号先算括号内的。比如对于表达式 3 + 5 × 2,应先计算乘法 5×2 = 10,再算加法 3 + 10 = 13。若式子中有多层括号,如(2 + 3)×(4 - 1),先算小括号内的 2 + 3 = 5 和 4 - 1 = 3,再算乘法 5×3 = 15。

整数运算
整数的加法和减法,数位对齐,从低位算起。如 325 + 147,个位 5 + 7 = 12,向十位进 1,十位 2 + 4 + 1 = 7,百位 3 + 1 = 4,结果是 472。乘法运算时,用一个因数的每一位去乘另一个因数,再把所得的积相加。例如 23×12,先算 23×2 = 46,再算 23×10 = 230,最后相加 46 + 230 = 276。除法运算要明确被除数、除数、商和余数的关系,如 75÷8,商是 9,余数是 3,因为 8×9 = 72,75 - 72 = 3。
小数运算
小数加减法要注意小数点对齐,也就是数位对齐。如 3.25 + 1.47,小数点对齐后,按照整数加减法计算,结果是 4.72。小数乘法先按照整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。比如 2.3×1.2,先算 23×12 = 276,因数共有两位小数,所以结果是 2.76。小数除法,当除数是整数时,按整数除法计算,商的小数点要和被除数的小数点对齐;当除数是小数时,要先把除数转化为整数,再计算。
分数运算
分数加法和减法,同分母分数相加减,分母不变,分子相加减。如 2/5 + 1/5 = 3/5。异分母分数相加减,先通分,化为同分母分数再计算。例如 1/2 + 1/3,通分后变为 3/6 + 2/6 = 5/6。分数乘法,分子相乘的积做分子,分母相乘的积做分母。如 2/3×3/4 = 6/12 = 1/2。分数除法,除以一个分数等于乘以它的倒数,如 2/3÷3/4 = 2/3×4/3 = 8/9。
掌握好数学表达式的计算方法,就能在数学的海洋中准确航行,解决各种数学问题。






















