在数学的世界里,函数的极限、导数和积分是至关重要的概念,它们在解决各种实际问题和理论研究中都发挥着关键作用。而maple软件为我们提供了强大而便捷的工具来计算这些数学量。
极限的计算
maple能够轻松地处理各种复杂函数的极限问题。无论是简单的多项式函数,还是包含三角函数、指数函数等的复杂组合函数,它都能迅速给出准确结果。比如,对于函数$f(x)=⁄frac{x^2 - 1}{x - 1}$,当$x$趋近于1时的极限,只需在maple中输入limit((x^2 - 1)/(x - 1), x = 1),瞬间就能得到极限值为2。这种高效准确的计算方式,大大节省了我们手动推导的时间和精力,让我们能够更专注于问题的分析和理解。
导数的求解
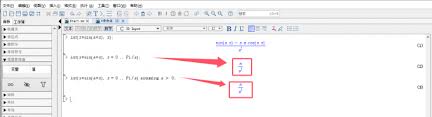
求函数的导数是研究函数变化率的重要手段。maple在导数计算方面表现卓越。它可以对各种初等函数以及复合函数进行求导。以函数$y = ⁄sin(x^2)$为例,在maple中输入diff(sin(x^2), x),就能快速得出其导数为$2x⁄cos(x^2)$。通过maple,我们可以深入了解函数的变化趋势,为进一步的分析和优化提供有力支持。

积分的运算
积分是微积分中的另一个核心内容。maple在积分计算上同样得心应手。它不仅可以计算常见函数的不定积分和定积分,对于一些特殊函数的积分也能给出精确结果。对于函数$f(x)=x^3 + 2x^2 + 1$在区间$[0, 1]$上的定积分,只需输入int(x^3 + 2*x^2 + 1, x = 0..1),就能得到积分值为$⁄frac{17}{12}$。这使得我们在处理积分问题时更加轻松,能够更高效地解决各种涉及积分的数学模型和实际问题。
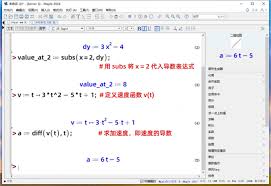
maple在函数的极限、导数和积分计算方面的强大功能,为数学学习、科研工作以及工程应用等领域带来了极大的便利。它让我们从繁琐的计算中解脱出来,将更多的精力投入到对数学本质的探索和应用场景的研究中,是我们不可或缺的数学计算利器。






















