maple软件作为一款强大的数学计算工具,在积分与极限的计算方面有着广泛的应用。
一、积分计算
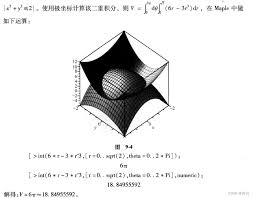
1. 不定积分
使用maple计算不定积分非常便捷。只需输入积分表达式,调用相应的积分函数即可。例如,对于⁄(⁄int x^2 ⁄sin x ⁄,dx⁄),在maple中输入int(x^2*sin(x),x),就能快速得到结果⁄(-x^{2}⁄cos ⁄left(x⁄right)+2⁄,⁄sin ⁄left(x⁄right)+2⁄,x⁄cos ⁄left(x⁄right)+c⁄)。
2. 定积分
计算定积分时,除了给出积分表达式,还需指定积分上下限。比如计算⁄(⁄int_{0}^{⁄pi} x ⁄sin x ⁄,dx⁄),输入int(x*sin(x),x = 0..pi),可得出结果⁄(⁄pi⁄)。
3. 多重积分
maple同样能轻松处理多重积分。例如对于二重积分⁄(⁄iint_{d} xy ⁄,da⁄),其中⁄(d⁄)是由⁄(x = 0⁄),⁄(x = 1⁄),⁄(y = 0⁄),⁄(y = x⁄)所围成的区域。在maple中输入int(int(x*y,y = 0..x),x = 0..1),即可得到结果⁄(⁄frac{1}{8}⁄)。
二、极限计算
1. 一元函数极限
求一元函数的极限时,使用limit函数。例如求⁄(⁄lim_{x ⁄to 0} ⁄frac{⁄sin x}{x}⁄),在maple中输入limit(sin(x)/x,x = 0),能迅速得出结果1。
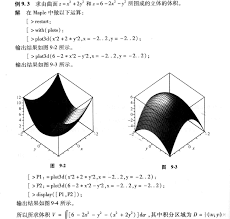
2. 多元函数极限
对于多元函数极限,如⁄(⁄lim_{(x,y) ⁄to (0,0)} ⁄frac{xy}{x^2 + y^2}⁄),maple也有相应的处理方法。输入limit((x*y)/(x^2 + y^2),(x,y)=(0,0)),可以通过一些特殊路径尝试来判断极限是否存在。当沿⁄(y = kx⁄)路径趋近时,代入化简后可得⁄(⁄frac{k}{1 + k^{2}}⁄),极限值与⁄(k⁄)有关,从而说明该极限不存在。
maple软件通过简洁高效的指令,为我们在积分与极限的计算中提供了极大的便利,无论是复杂的表达式还是多元函数的相关计算,都能快速准确地得出结果,是数学学习和研究中的得力助手。






















