maple是一款功能强大的数学软件,其微分命令在数学计算和分析中发挥着重要作用。
基本微分命令
maple中求函数导数的基本命令是diff。例如,对于函数$f(x)=x^2$,要求其导数,只需输入diff(x^2,x),即可得到结果2*x。这一命令可以方便地处理各种初等函数的求导问题,无论是多项式函数、三角函数、指数函数还是对数函数等,都能准确快速地给出导数表达式。
高阶导数
通过多次使用diff命令,能够轻松求出高阶导数。比如求函数$y = ⁄sin(x)$的二阶导数,输入diff(sin(x),x,x),就能得到$-⁄sin(x)$。对于复杂函数,高阶导数的计算也不在话下,它会按照求导法则逐步计算,清晰地呈现出每一步的结果,为深入研究函数的性质提供有力支持。
多元函数微分
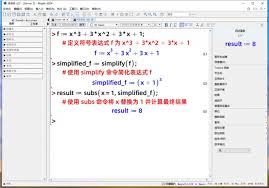
在处理多元函数时,maple同样表现出色。假设$z = f(x,y)=x^2 + y^2$,求关于$x$的偏导数,输入diff(x^2 + y^2,x),可得2*x;求关于$y$的偏导数,输入diff(x^2 + y^2,y),得到2*y。若要求二阶混合偏导数,如diff(diff(x^2 + y^2,x),y),会准确得出结果2。maple严格遵循多元函数求导的链式法则和混合偏导数相等的定理,确保计算结果的准确性。
隐函数微分
对于由方程确定的隐函数,maple也能进行微分运算。例如,对于方程$x^2 + y^2 = 1$确定的隐函数$y(x)$,求$y^⁄prime$,可以使用隐函数求导命令。先使用implicitdiff命令,输入implicitdiff(x^2 + y^2 = 1,y,x),就能得到$-x/y$,方便快捷地解决了隐函数求导的难题。
maple的微分命令为数学研究和工程计算等领域提供了极大的便利。无论是基础的导数计算,还是复杂的高阶导数、多元函数微分以及隐函数微分,它都能准确无误地完成,帮助用户高效地探索数学问题,推动数学和相关领域的发展。