在数学的奇妙世界里,反函数是一个独特而有趣的存在。它不仅为我们解决问题提供了新的视角,还在许多领域有着广泛的应用。而maple作为一款强大的数学软件,为我们求反函数提供了便捷且高效的方法。
一、理解反函数的概念
在深入学习如何在maple中求反函数之前,我们先来简单回顾一下反函数的概念。对于一个函数y = f(x),如果存在另一个函数x = g(y),使得对于f(x)定义域内的任意x,都有g(f(x)) = x,并且对于f(x)值域内的任意y,都有f(g(y)) = y,那么g(y)就是f(x)的反函数,通常记作f^(-1)(y)。
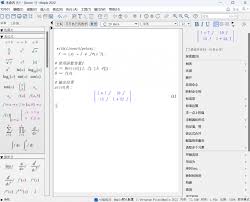
二、maple中求反函数的基本方法
1. 使用solve函数
在maple中,solve函数是求反函数的常用工具。例如,对于函数y = 2x + 3,我们可以这样求它的反函数:
首先定义原函数:f := x -> 2*x + 3;
然后使用solve函数求解反函数:inverse_f := solve(y = f(x), x);
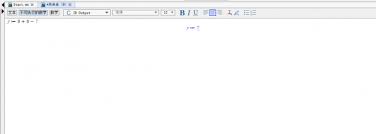
执行上述代码后,maple会给出反函数的表达式:inverse_f := (-3 + y) / 2,即f^(-1)(y) = (y - 3) / 2。
2. 利用implicitdiff函数
对于一些复杂的函数,直接求解反函数可能比较困难,这时我们可以借助implicitdiff函数。例如,对于方程x^2 + y^2 = 1,我们想求y关于x的反函数。
首先定义方程:eq := x^2 + y^2 = 1;
然后使用implicitdiff函数:diff(eq, x, y);
maple会给出 -x / y,这其实就是隐函数形式下y关于x的导数,通过进一步的推导可以得到反函数的相关信息。
三、示例与应用
让我们来看一个实际的例子,假设我们有一个函数y = x^3 + 2x - 1,要求它的反函数。
定义原函数:f := x -> x^3 + 2*x - 1;
使用solve函数求反函数:inverse_f := solve(y = f(x), x);
maple会给出反函数的表达式,虽然可能看起来比较复杂,但它准确地表示了原函数的反函数关系。
在实际应用中,反函数在物理学、工程学、经济学等领域都有着重要的作用。比如在电路分析中,通过求某些函数的反函数可以更好地理解电路参数之间的关系;在经济学中,反函数可以帮助分析成本与收益之间的变化规律。
总之,maple为我们求反函数提供了强大的支持,无论是简单函数还是复杂函数,都能通过合适的方法得到准确的反函数表达式,从而帮助我们在数学的探索中更加得心应手,解锁更多的知识奥秘。






















